数据结构与算法
Created|Updated
|Post Views:
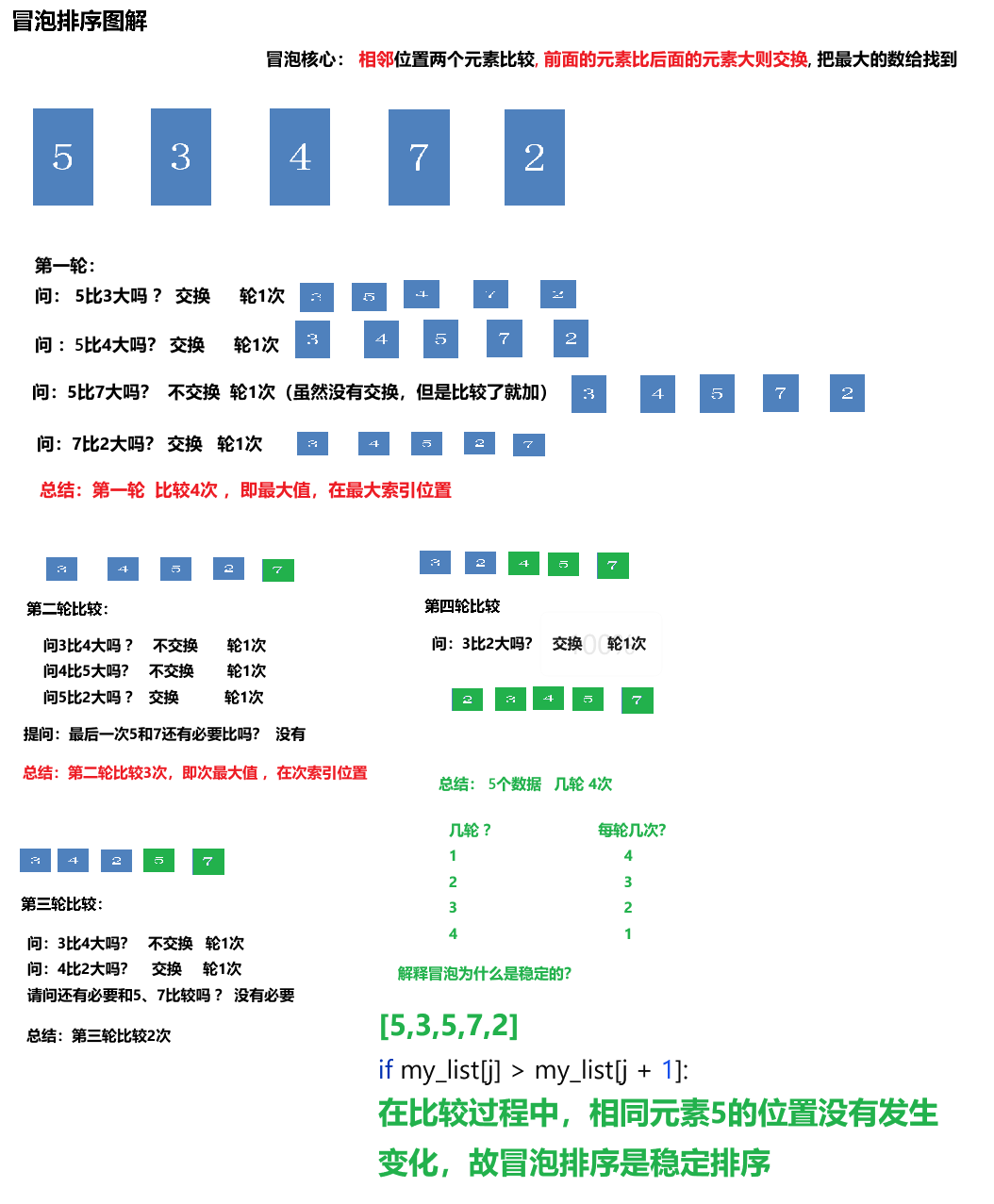
冒泡排序_思路及代码
1 | """ |
选择排序_思路及代码
思路分析
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44"""
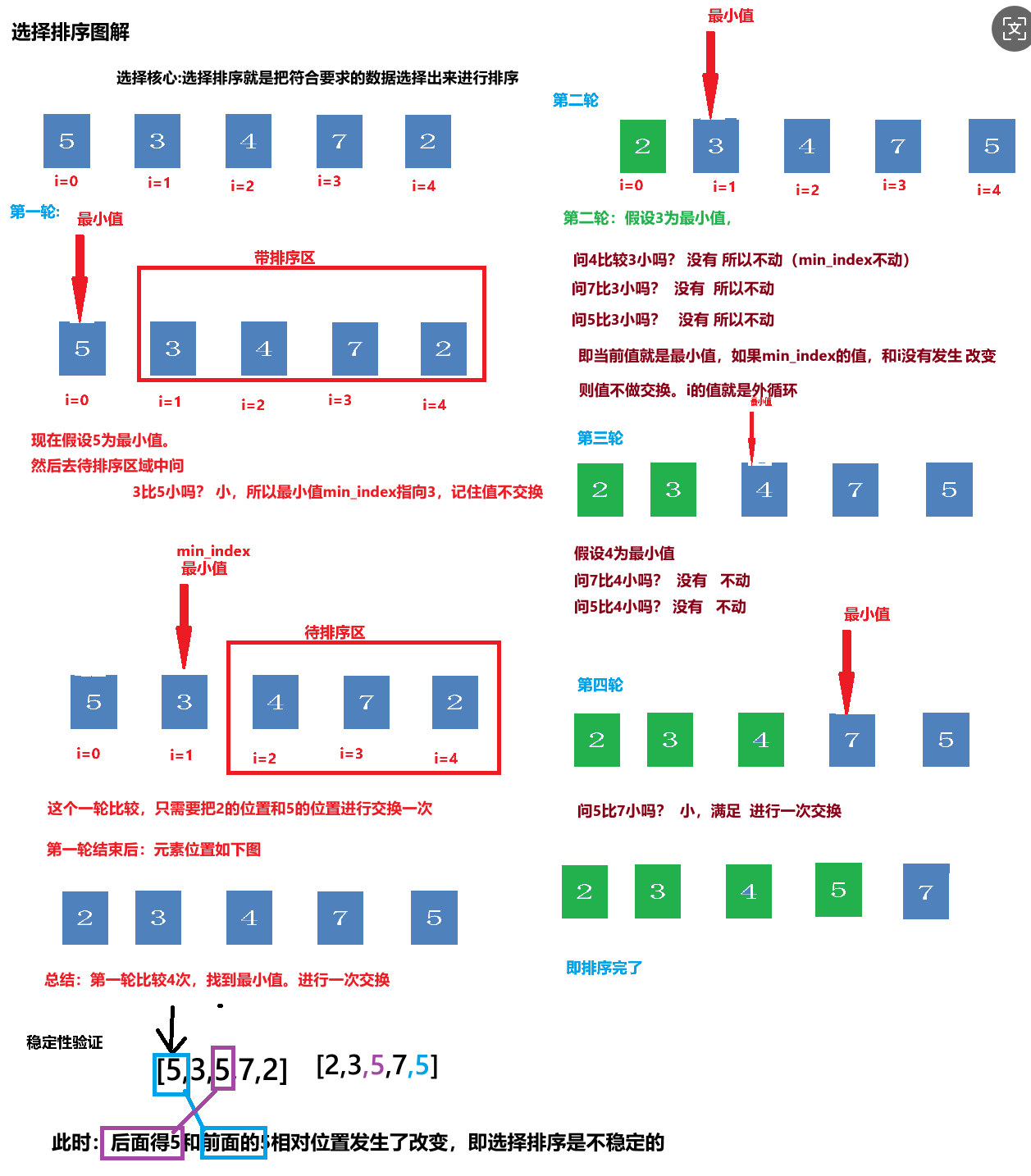
选择排序介绍:
原理:
每轮都假设该轮最前面的那个元素为最小值,然后去 剩下的列表中去寻找真正的最小值。
最终交换即可。这样就找到了本轮的最小值。重复以上步骤即可。
大白话:
第一轮,假设i=0位置的元素是最小值。然后用min_index记住他索引,然后去剩下的所有元素中
寻找最小值,找到了用min_index做记录。最终判断i和min_index是否交换。第一轮完毕后。
最小值就在最小索引处。 重复该步骤,直至排序完成。
分析流程:
假设5个元素
第几轮(索引) 该轮比较总次数 公式(具体的谁和谁比较)
第一轮(0) 4次 索引0和1,2,3,4比较
第二轮(1) 3次 索引1和2,3,4比较
第三轮(2) 2次 索引2和3,4比较
第四轮(3) 1次 索引3和4比较
要点:
1:比较的总轮数 列表长度-1
2:每轮比较总次数 i+1 ~列表长度
3:谁和谁比较? 索引min_index(初始i)和索引j比较,索引i和索引min_index的值交换
"""
def select_sort(my_list):
# 获取列表长度
n = len(my_list)
# 外层循环控制比较轮数
for i in range(n - 1):
# 定义变量min_index,记录本轮最小值的索引
min_index = i
# 内循环控制 每次比较轮数:次数
for j in range(i + 1, n): # 1234 234 34 4
# 具体的比较过程,索引min_index和索引j比较
if my_list[j] < my_list[min_index]:
min_index = j
# 走到这里了。说明本轮已经找到最小值了,判断,并交换
if min_index != i:
my_list[min_index], my_list[i] = my_list[i], my_list[min_index]
if __name__ == '__main__':
my_list = [5, 3, 4, 7, 2]
print(f"排序前:{my_list}")
select_sort(my_list)
print(f"排序后:{my_list}")
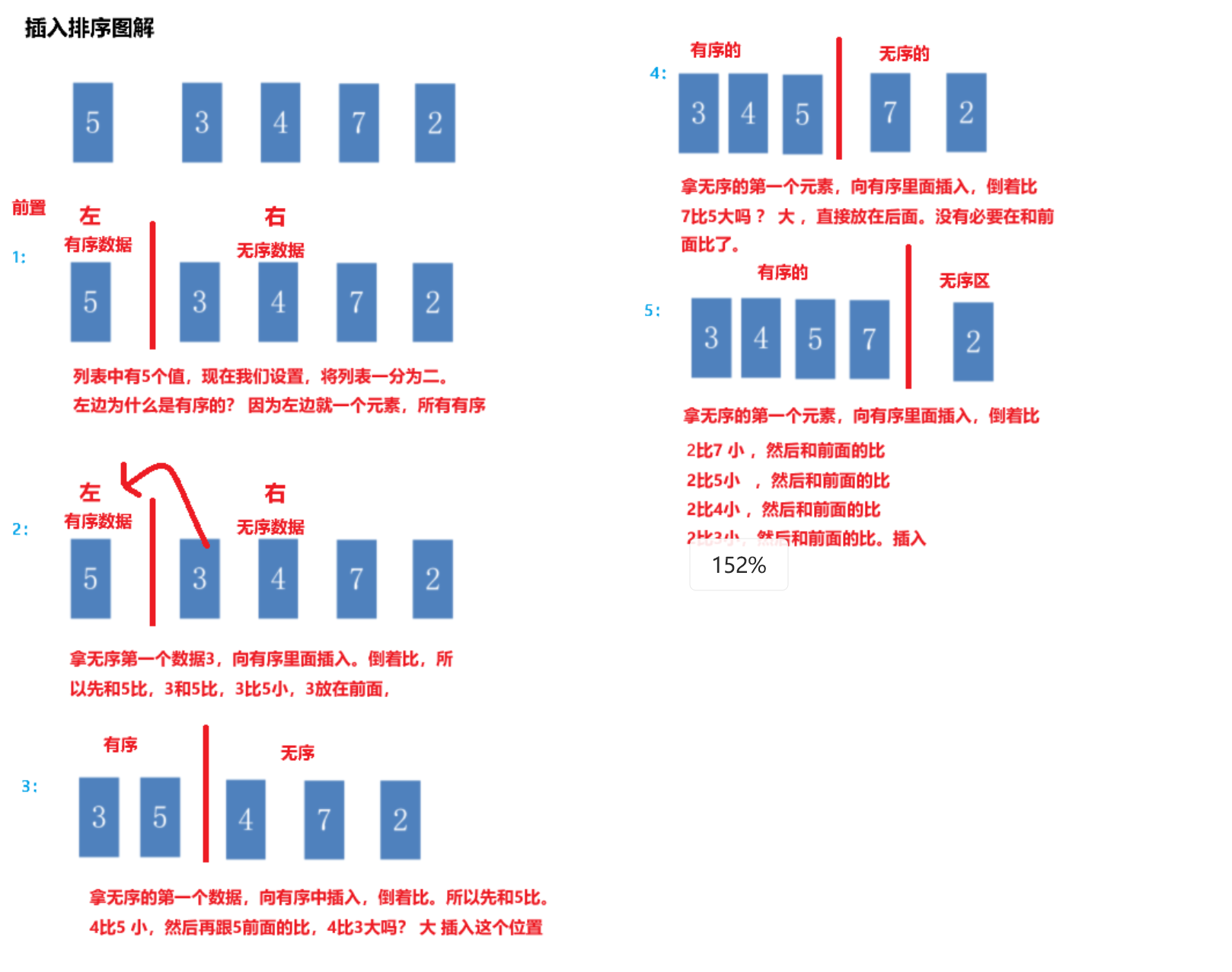
插入排序_思路及代码
1 | """ |
二分查找
1 | """ |
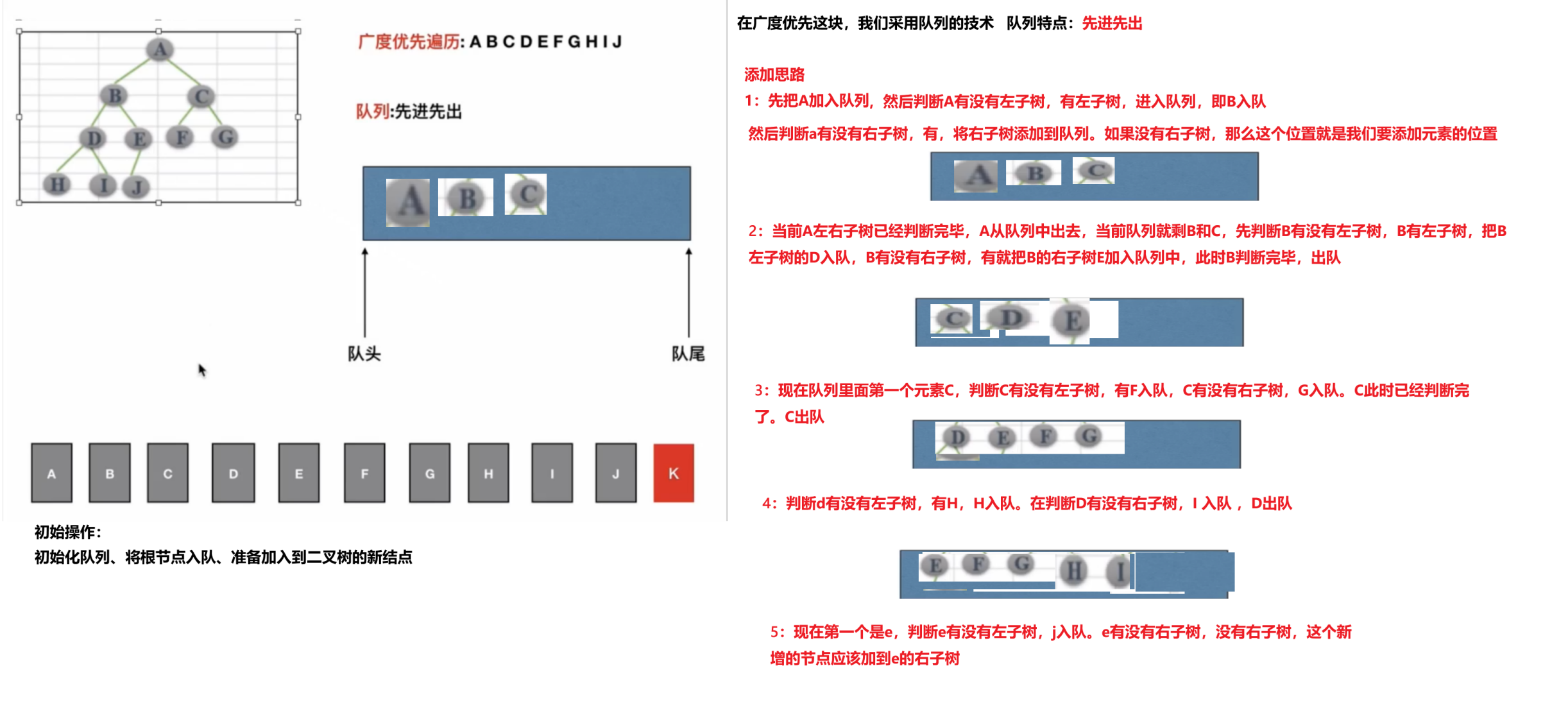
自定义代码模拟二叉树
图解
代码框架
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181# 定义Node类,表示二叉树节点
class Node:
# 初始化属性
def __init__(self, item):
self.item = item
self.lchild = None
self.rchild = None
# 自定义BinaryTree ,表示二叉树
class BinaryTree:
def __init__(self, node=None):
self.root = node
# 定义add函数,表示添加节点
def add(self, item):
# 1.item封装为节点
new_node = Node(item)
# 2.判断根节点是否为null,如果为空,设置当前节点为跟节点
if self.root is None:
self.root = new_node
return
# 3.创建一个队列,添加根节点到队列中
queue = []
queue.append(self.root)
# 4.通过while True 死循环 找到空缺的节点位置
while True:
# 5.获取队列第一个元素
node = queue.pop(0)
# 6.判断当前节点左子树是否为空
if node.lchild is None:
# 6.1把新节点当做当前节点的左子树,并结束
node.lchild = new_node
return
else:
# 6.2走到这里,说明左子树不为空,把当前节点的左子树添加队列中
queue.append(node.lchild)
# 7.判断当前节点的右子树是否为空
if node.rchild is None:
# 7.1把新节点设置为当前节点的右子树 ,并结束
node.rchild = new_node
return
else:
# 走到这里,说明右子树不为空,把当前节点的右子树,添加到队列中
queue.append(node.rchild)
# 定义遍历二叉树 广度优先遍历 (逐层遍历,一层一层的遍历)
def breadth(self):
# 1.判断根节点是否为空
if self.root is None:
return
# 2.创建队列
queue = []
queue.append(self.root)
# 3.循环打印内容
while len(queue) != 0:
# 4.获取第一个元素
node = queue.pop(0)
# 5.打印该节点的元素域
print(node.item, end=" ")
# 6.判断当前节点的左子树是否存在,存在添加到队列中
if node.lchild is not None:
queue.append(node.lchild)
# 7.判断当前节点的右子树是否存在,存在添加到队列中
if node.rchild is not None:
queue.append(node.rchild)
# 深度优先之先序遍历(根左右)
def preorder(self, root):
# 1.判断根节点是否不为空,不为空才打印
if root is not None:
print(root.item, end=" ")
# 递归遍历左子树
self.preorder(root.lchild)
# 递归遍历右子树
self.preorder(root.rchild)
# 深度优先之中序遍历(左根右)
def inorder(self, root):
# 1.判断根节点是否不为空,不为空才打印
if root is not None:
# 递归遍历左子树
self.inorder(root.lchild)
print(root.item, end=" ")
# 递归遍历右子树
self.inorder(root.rchild)
# 深度优先之后序遍历(左右根)
def postorder(self,root):
if root is not None:
#遍历左子树
self.postorder(root.lchild)
#遍历右子树
self.postorder(root.rchild)
#打印根节点
print(root.item,end=" ")
def dm1_1_测试节点和二叉树类():
# 1-创建节点
node1 = Node("A")
# 打印节点的元素域 左子树 右子树
print(node1.item) # a
print(node1.lchild) # None
print(node1.rchild) # None
print("--------二叉树类----------")
# #创建了一个空树
# bt = BinaryTree()
# print(bt.root) #None
print("--------测试二叉树----------")
bt = BinaryTree(node1)
print(bt.root) # <__main__.Node object at 0x000001E7F19438B0>
print(bt.root.item)
print(bt.root.lchild)
print(bt.root.rchild)
def dm2_2_测试添加节点():
bt = BinaryTree()
# 添加元素
bt.add("A")
bt.add("B")
bt.add("C")
bt.add("D")
bt.add("E")
bt.add("F")
bt.add("G")
bt.add("H")
bt.add("I")
bt.add("J")
def dm3_3_测试添加_遍历节点():
bt = BinaryTree()
# 添加元素
bt.add("A")
bt.add("B")
bt.add("C")
bt.add("D")
bt.add("E")
bt.add("F")
bt.add("G")
bt.add("H")
bt.add("I")
bt.add("J")
bt.breadth()
def dm4_4_测试深度优先_先序遍历节点():
bt = BinaryTree()
# 添加元素
bt.add("A")
bt.add("B")
bt.add("C")
bt.add("D")
bt.add("E")
bt.add("F")
bt.add("G")
bt.add("H")
bt.add("I")
bt.add("J")
print("先序遍历(根左右)")
bt.preorder(bt.root)
print()
print("中序遍历(左根右)")
bt.inorder(bt.root)
print()
print("后序遍历(左右根)")
bt.postorder(bt.root)
if __name__ == '__main__':
# dm1_1_测试节点和二叉树类()
# dm2_2_测试添加节点()
# dm3_3_测试添加_遍历节点()
dm4_4_测试深度优先_先序遍历节点()根据中序和先序_逆推二叉树结构

Author: 甘虎文
Copyright Notice: All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
Related Articles
2023-09-29
数据结构与算法1
数据结构和算法简介 数据结构 就是存储和组织数据的方式, 分为: 线性结构 和 非线性结构 算法 就是解决问题的思路和发放, 它具有独立性, 即: 它不依赖语言, 而是解决问题的思路. Java能做, Python也能做. 特性 有输入, 有输出, 有穷性, 确定性, 可行性. 如何衡量算法的优劣 ==大O标记法,== 即: 将次要条件都省略掉, 最终形成1个表达式. **主要条件:**随着问题规模变化而==变化==的. **次要条件:**随则问题规模变化而==不变==的. 最优和最坏时间复杂度 如非特殊说明, 我们考虑的都是 最坏时间复杂度, 因为它是算法的一种保证. 而最优时间复杂度是算法的 最理想, 最乐观的状况, 没有太大的参考价值. 常见的时间复杂度如下 从最优到最坏分别是: O(1) -> O(logn) -> O(n) -> O(n logn) -> O(n²) -> O(n³) ...
2023-08-09
生成器_正则
多线程特点_随机性12345678910111213141516171819202122import threading# 使用多线程来模拟小明一边编写num行代码,一边听count首音乐功能实现。def coding(name, num): for i in range(num): print(f"{name}正在敲{i}行代码")def music(name, count): for i in range(count): print(f"{name}正在听{i}遍音乐")# args 元组# kwargs 字典if __name__ == '__main__': t1 = threading.Thread(target=coding, args=("小明", 100)) t2 = threading.Thread(target=music, args=("小...
2023-10-31
网络编程_进程_线程
网络编程介绍 概述 就是用来实现网络互联的 不同计算机上 运行的程序间 可以进行数据交互. 三要素 IP地址: 设备(电脑, 手机, Ipad…)在网络中的唯一标识 分类: IPV4, 4字节, 十进制. 例如: 192.168.88.100 IPV6, 8字节, 十六进制, 宣传语: 可以让地球上的每一粒沙子都有自己的IP 两个DOS命令: 查看IP: windows: ipconfig Linux, Mac: ifconfig 测试网络连接: ping ip地址 或者 域名 端口号: 程序在设备(电脑, 手机, Ipad…)上的唯一标识. 范围: 0 ~ 65535, 其中0 ~ 1023已经被系统占用或者用作保留端口, 自定义端口时尽量规避这个范围. 协议: 传输规则, 规范. 常用的协议: TCP(这个用的最多) 和 UDP TCP特点: 1.面向有连接 2.采用字节流传输数据, 理论无大小限制. 3.安全(可靠)...
2023-05-02
闭包_装饰器_深浅拷贝
闭包背景介绍12345678910111213141516171819"""案例目的: 引出闭包相关知识点"""# 定义一个函数用于保存变量10,然后调用函数返回值变量并重复累加数值,观察效果。def func(): num = 10 return numnum = func()print(num + 1) # 11 想要结果是 11print(num + 1) # 11 vs 12print(num + 1) # 11 vs 13# 你会发现无法实现累加!那么如何实现累加呢!! 闭包 闭包入门 12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758# 定义一个用于求和的闭包。# 其中,外部函数有参数num1,内部函数有参数num2,# 然后调用,并用于求解两数之和,观察效果"&qu...
2023-06-03
面向对象基础
面向对象和面向过程 编程思想 就是人们利用计算机来解决问题的思维. 分类 面向过程 它是一种编程思想, 强调的是以 步骤(过程) 为基础完成各种操作. 面向对象 参考思路: 概述, 思想特点, 举例, 总结 它是一种编程思想, 强调的是以 对象 为基础完成各种操作, 它是基于 面向过程的.说到面向对象, 不得不提的就是它的三大思想特点: 1. 更符合人们的思考习惯. 2. 把复杂的事情简单化. 3. 把人们(程序员)从执行者变成指挥者. 举例: 越符合当时的场景越好, 例如: 买电脑, 洗衣服… 总结: 万物接对象. 面向对象特征介绍 三大特征 封装 继承 多态 封装简介 概述 就是隐藏对象的属性和实现细节, 仅对外提供公共的访问方式. 举例 电脑, 手机, 函数, 类 = 属性 + 行为 好处 提高代码的安全性. (私有化) 提高代码的复用性. (函数) 继承 概述 子类继承父类的成员, 例如: 属性, 行为等.大白话: 子承父业. 好处 提高代码的复用性. 多态...
2023-07-07
面向对象进阶
子类重写父类的功能12345678910111213141516171819202122232425262728293031323334353637# 小明掌握了老师傅和黑马的技术后,# 自己潜心钻研出一套自己的独门配方的全新摊煎饼果子技术。"""重写解释: 概念:重写也叫覆盖,即子类出现和父类【重名】的属性或者方法 。称之为重写 调用层次:就近原则 子类用子类的,没有就去找父类的,依次按照继承顺序去找其他父类"""class Master: def __init__(self): self.kongfu = "[古法煎饼果子配方]" def make_cake(self): print(f"运用{self.kongfu}制作煎饼果子")class School: def __init__(self): self.kongfu = "[黑马AI煎饼果子配方]" de...